淀川区・新北野中・北野高校そばの学習塾エイ・ステーション池上です。
前半は新年度のお知らせなどですので、不要な方は↓へ
塾長がお手伝いしているイベントです。↓興味ありましたらお越しください。
1つ前の記事の続きです。
【大問3】
身近なものを関数にしてみましたシリーズ。
一般も出ますが、ほぼ100%１次関数です。y=ax+bです。
ただし、たまに表ではなくてグラフ形式の問題になることがあります。
1)②からやってください。
切片→x=0のときのyの値なので190
傾き→xが1増えたときのyの増加量なので7
y=ax+bに代入してやってもいいですが、数字が大きいと計算間違う可能性高くなるので注意。
②の式ができたら、①に戻って代入して表を埋めましょう。
③も代入するだけ。
2)連立方程式。500円玉をa枚、100円玉をb枚とします。
枚数で式を作ると、a+b=37
重さで式を作ると、7a+4.8b+190=394
あとは計算ミスのないように解きましょう。
上の式を変形して代入法でやる方が簡単かなと思います。
連立方程式を解いたら、枚数から金額を求めましょう。
枚数だけ求めて終わらないように、何を聞いているか確認して答えを書きましょう。
【大問4】
平面図形折り紙シリーズ。折り紙とは書いてませんが、合同な図形が隣り合っていて折り紙のパターンですね。
1)①∠EFG=∠EFB
∠EFBは四角形ABFEの内角から求められます。360°から90°2つとa°をひき算です。
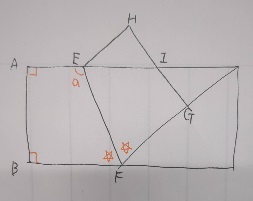
②相似の証明。詳しくは省略しますが、相似の証明はほぼ「2角がそれぞれ等しい」のパターンですね。等しい角度や長さを図に書き込んで見つけましょう。お絵描きしない受験生に人権はないの格言もあります。
2)①まずはわかっている長さを全部書き込みましょう。
前の問題の1)②の相似を利用します。手前に相似か合同の証明問題があれば、それを利用して次を解けというサインだと思ってください。
比を作るのにDFの長さが足りないので、△DCFの三平方で求めましょう。
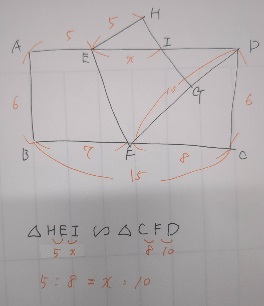
②まず①で求めた長さを図に書き込みましょう。
△EIJ∽△FBJで、相似比は25/4：7=25:28 つまり、EJ:JF=25:28
△AEJ∽△KFJで、相似比はEJ:JFと同じ25:28
よって、AE:FK=25:28となるので、FKが求められます。
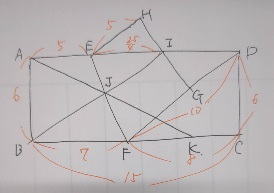
では。
体験授業や教室での面談など、詳しくはLINEやメールでお問い合わせください。
インスタもお願いします↓
