淀川区・新北野中・北野高校そばの学習塾エイ・ステーション池上です。
前半は新年度のお知らせなどですので、不要な方は↓へ
塾長がお手伝いしているイベントです。↓興味ありましたらお越しください。
先月行われた2024年大阪府公立高校入試の特別選抜の問題を解いてみました。
一般入試の参考にどうぞ。
【大問１】
1)かけ算を先に。途中式書こうね。
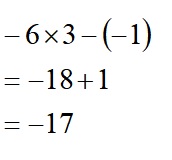
2)二乗のところ先に。途中式書こうね。
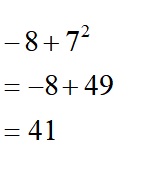
3)カッコ外すときにミスらないように。特に後ろ側。途中式書こうね。
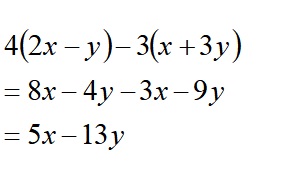
4)約分ミスらないように。約分の数字は「上下」に大きく書きましょう。ナナメに書くと見落としがち。
18の真上に9、bの2乗の前にbを書きましょう。
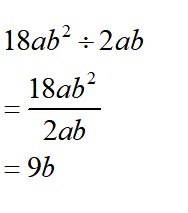
5)展開の公式を覚えていれば簡単。2行目の式（後ろだけカッコになっているところ）をきちんと途中式書けるかがポイント。書かないとミスします。
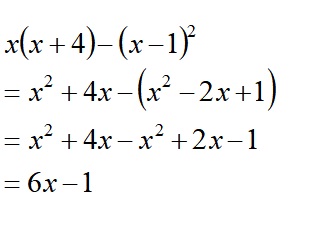
6)ルートの中身を小さくする、有理化と約分ができるかどうか。ルートは中身の数字が小さくできるかどうか最後に確認すること。
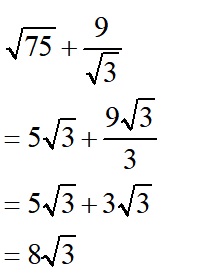
【大問2】
1)ルートの大きさを比べるときは、整数でサンドイッチ。先にルートの部分だけやって、-2はあとでたし算。
よって、答えは1と2の間のところ。
2)「yはxに反比例し～」とあったら無意識のうちに、「y=a/x」を1行目に書いて下さい。
あとは代入して計算するだけ。
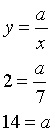
3)方程式の分数はかけ算して分母を消してしまいましょう。途中式の2行目（カッコのところ）を書かないと間違えます。ちなみに「計算しましょう」問題の分数は消しちゃダメ。
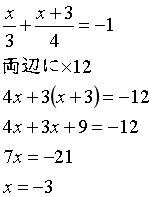
4)因数分解するパターン。解の公式パターンや平方根パターンも復習しておきましょう。
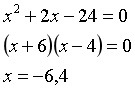
5)データの問題
ア…相対度数＝度数÷合計を計算すると、0.3…なので×
イ…30回以上は3人なので×
ウ…範囲はこの表からは判断不可なので×
エ…中央値は7人目→27～30の階級なので○
6)確率。表を作りましょう。
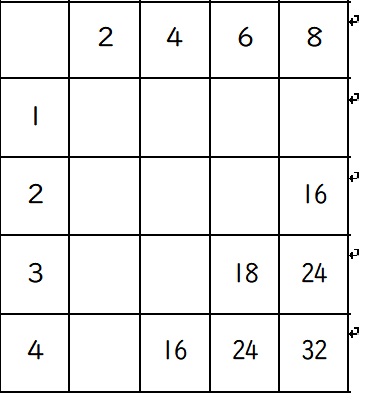
サイコロ以外でも数字のカードも表が有効です。
7)30°の直角三角形なので三平方の定理で、AB=4√3、AC=8
また、BからACにおろした垂線の足をHとすると、BH=2√3、AH=8、CH=2
Aを頂点とする円錐の体積+Cを頂点とする円錐の体積なので、
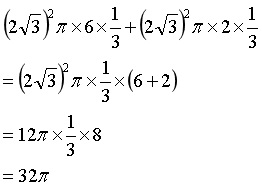
結合法則的な計算の工夫使うとはやいですね。
8)まず、グラフ上にわかる座標を書きましょう。
直線の式は問題からわかります。傾きと切片(=y軸と交わるところ)が書いています。
Bのx座標はとりあえずbにして、B(b, -1)
これを直線の式に代入すると、bの値がわかります。
Aのy座標はBより5大きいので、A(b, 4)
bは計算済みなので、これを二次関数の式に代入するとaも求められます。
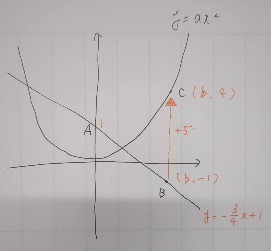
二次関数は必ず1問は出るので、グラフに座標や式を書き込んで考えてください。
わからんところは文字にして方程式を作ります。
答えがまあまあ変な分数になりがちですが、ビビらないように。
B面は次の記事で（朝9時にアップします）
では。
体験授業や教室での面談など、詳しくはLINEやメールでお問い合わせください。
インスタもお願いします↓
